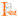Heterogeneity Revolution in Behavioural Economics Public Policy? Does God Play Dice with Universe?
Behavioural Insights Units have been emerging across the world. The first behavioural insights unit, or ‘nudge unit’, was started in a probing fashion when David Cameron was the Prime Minister of the United Kingdom. Pronto far and wide, a unit appeared entangled with the questions on how to make people behave better. There are 202 institutions recognised by the OECD to apply behavioural insights in public policy. Apart from national units, states are also shifting towards policy-making from a perspective of behavioural science, for example, in Uttar Pradesh.
Despite these advances, the credibility of behavioural science came into question with the replication crisis. With the increasing use of behavioural insights, one of the challenges that surface with it – it is specious.
A recent paper by Christopher J. Bryan, Elizabeth Tipton, and David S. Yeager published in Nature human behaviour led to four hypothetical experiments contending the efficacy of behavioural interventions. The complete study can be found here.
What were the four hypothetical experiments?
Study 1: (Graph a) In this hypothetical study, the sample consists of a highly responsive portion of the population (for ex., students). Study 2: (Graph b) The sample covers a broader range of subpopulations and contexts – responsive and less responsive portions of the population. Study 3: (Graph c) This study had an entirely different sample from the previous studies, with different contexts and not naturally responsive. Study 4: (Graph d) A hypothetical study with a representative population sample.
All four hypothetical experiments evaluate the same behavioural intervention. Each dot represents the treatment effect for an individual. The shaded slices represent the sample from the population. What is interesting to note here, as the sample differs, the average treatment effect also begins to differ. To find if the intervention can work for all, in the third hypothetical experiment, the average treatment effect was found to be almost negligible in the same experiment with an entirely different population (Graph c). This represents a failure to replicate. Considering that the sample size is larger in graph c than in graph a, these findings may get more credibility, concluding that the first experiment is a false positive. But what is also surprising is that the fourth hypothetical experiment (Graph d), which has a representative sample of the entire population, estimates the average treatment effect to be 0.07 roughly, which may not be considered sufficient. If we consider the main effect, we will miss the fact that there is a sizable population (Graph a) for whom the effect is significant and evidence to be used in a policy-making perspective. So while this particular intervention may not be helpful for all the population, it is still effective in a specific context of people.
A heterogeneous approach to behavioural interventions can contribute significantly if this population is vulnerable. Replication crises crumpled bodies of research. And the policy victories due to behavioural interventions in the past soon disappointed when implemented on a large scale. This study demonstrated why the ‘one size fits all’ approach is least likely to work in behavioural interventions. There is an increasing need to recognise the heterogeneity in society. These findings raise pivotal questions. With mounting use of existing non-heterogenous results, how do we ensure fairness in policy-making?
For example, in a diverse country like India, the social reality differs after every 50 miles. The need for interdisciplinary scholars who can think of rich ways to include culturally and demographically divergent circumstances is essential. Despite the initial promising findings from the discipline, the concluding generality seems precarious. Studies have also highlighted that what worked on a local scale may not work on a larger or national scale.
We need more skin in the game by safeguarding the accountability of behavioural units in policy-making. It is clear that depending on a large sample alone may not meaningfully explain the empirical findings. We need to maintain skepticism when we see studies with large sample sizes; they may not be ensuring heterogeneity. Even if they were, it is most likely that those interventions were more effective in wealthy, western, and educated populations. This problem may not be limited to one discipline alone; similar issues may also exist in other social science disciplines. But to make a case of behavioural science transforming the world, as the authors in the study demonstrated, we need a heterogeneity revolution.
“Of course, the broader behavioural science community is no stranger to heterogeneity in treatment effects. There is a large and diverse literature documenting the ways in which social identity, culture or life circumstances, for instance, can cause people to understand and respond to identical stimuli in very different ways. And the two-by-two experiment has long been a staple of basic laboratory research in social psychology. These (and other) research traditions provide a basis for predicting, understanding, and harnessing the probative power of heterogeneous effects in behavioural intervention research. The nascent heterogeneity revolution will build on the strengths of these existing research traditions by complementing the theoretical interest in context- and group-based differences with sampling methods that can yield generalisable insights about those differences.”
Let me attempt to justify Louis Bachelier's claim by building a suitably logical narrative on how gambling has led to the invention of probability theory which in turn explains so much of the world around us. The way I see it, the gambling dens of Europe have been directly responsible for the invention of probability theory. How did that come about? It has so happened that in the seventeenth century, professional gamblers began to perceive that there was a mathematical method to the games of chance that were in fashion. One of these enterprising gamblers had the wisdom to bring the matter to the attention of two outstanding mathematicians, Pascal and Fermat. Both these individuals-geniuses that they were-could perceive the mathematical principles that were underlying the outcomes of games of chance. And thus, probability theory was brought into existence. Of course, in the course of time it has evolved and gone way beyond its applications to gambling and has now come to occupy a central position in terms of explaining the world around us. But its moorings are rooted in gambling. And what are the areas and realms of enterprise where probability theory plays a central role? The rest of this article shall strive to build a story-in absolutely non-technical terms-on the major role that probability occupies in our lives today.
Let me begin the story by looking at a very fundamental notion which, despite having strong mathematical moorings, is used in our daily conversations without much realization of this deeper mathematical connection. I speak of the concept of randomness. It is commonplace to hear this word being bandied about. What does the word random mean? Our everyday understanding and use of the term denotes the inability to detect information or a pattern based on which some sort of predictability of the occurrence of the event can be devised. The easiest illustration of this is the inability to predict the outcome when a fair coin is tossed. Although there can only be one of two outcomes-a head or a tail-no one can predict with certainty the actual outcome. This is probably the easiest illustration of a random event. Does this mean that randomness cannot be harnessed? The exact opposite is true. Let us hark back to the business of coin tossing. Even though no one can predict the outcome of a single toss of a fair coin we can still do much with it. Most of us are familiar with the phrase ‘the odds of a head occurring are half’.
The easiest way to explain this is by means of the statement that if a coin were to be tossed a very large number of times and the outcomes counted then about half the number of times the outcome will be seen to be head. Anyone who has the patience and skill to toss a coin a few thousand times can actually see this phenomenon for herself. A person adept at coding can easily devise an experiment which shall demonstrate the truth of my assertion in no time. Thus, even when we are not in a position to predict the outcome of a single toss of a coin, we can see that a certain degree of predictability or pattern does emerge even out of this random event. Randomness is therefore of much practical use. If in today’s times, I need to fathom the chance of an individual in Delhi being infected with Covid-19. I could do so through a fairly accurate method. All I need to do is pick a random sample of the population of Delhi and count the number of people in this population is infected with the virus. This shall give me the probability of an individual being infected with the virus or a fairly good estimate of the number of people in the entire population being infected with the virus. Actually, much greater accuracy can be built into the experiment but I do not wish to be technical.
Randomness exists everywhere around us and the use of probability theory helps us to demystify much of our world. Einstein used the phenomenon of Brownian motion to demonstrate the existence of atoms. Brownian motion is the behaviour of very small particles suspended in a medium such as a liquid or a gas. Brownian motion is very well explained through probability. The amazing thing is that some of the deepest theories of pure mathematics have been discovered through Brownian motion. Paraphrasing and perhaps also oversimplifying the words of the great physicist Feynmann, nature is only to be explained in terms of probabilities when we are looking at things on a very small scale. Thus, the behaviour of an electron is best understood through the lens of probability.
There is, therefore, a chance involved. And hence, it seems that God is indeed playing dice with us contrary to what Einstein believed.
Contribution by Fazli